계수 정렬 (Count Sort) 은 매우 빠른 정렬 알고리즘이다. 그러나 한 가지 치명적인 약점이 있는데 바로 특정한 조건이 부합할 때만 사용할 수 있다는 것이다. 그 약점은 바로 '데이터의 크기 범위가 제한되어 정수 형태로 표현할 수 있을 때만 사용가능하다' 라는 것이다. 만약 데이터가 무한한 범위를 가질 수 있는 실수형 데이터라면 이 계수 정렬을 사용하기 힘들다는 것이다. 또한 일반적으로 가장 작은 데이터와 가장 큰 데이터의 값의 차이가 1,000,000을 넘지 않을 때 효과적으로 사용할 수 있다.
계수 정렬은 일반적으로 별도의 리스트를 선언하고 그 안에 정렬에 대한 정보를 담는다는 특징이 있다. 즉, 앞서 다루었던 정렬 알고리즘과는 다르게 직접 데이터의 값을 비교한 뒤에 위치를 변경하는 정렬 방식(비교 기반의 정렬 알고리즘)이 아니라는 것이다. 계수 정렬은 별도의 리스트를 선언한다고 했는데 이 리스트는 모든 범위를 담을 수 있는 크기의 리스트여야 한다. 만약 최소 데이터와 최대 데이터의 값의 차이가 1,000,000이라면 0 ~ 1,000,000을 모두 담아야 하므로 1,000,001 의 크기의 리스트를 선언해야 한다는 것이다.
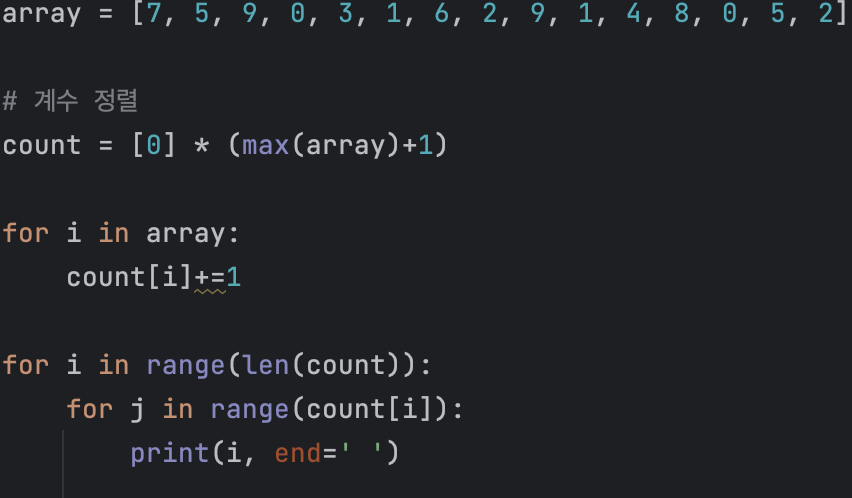
아래와 같은 데이터를 계수 정렬하는 과정을 살펴보자.
7 5 9 0 3 1 6 2 9 1 4 8 0 5 2
여기서 가장 큰 데이터는 9, 가장 작은 데이터는 0 이므로 0 ~ 9 를 표현할 크기가 10인 리스트를 새로 선언한다.
이후 각 데이터의 개수를 카운트해서 새로 선언한 리스트에 저장하는 것이다. 이 과정을 거치면 새로 선언한 리스트에는 아래와 같은 값이 저장된다.
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 2 | 2 | 2 | 1 | 1 | 2 | 1 | 1 | 1 | 2 |
결과적으로 위의 리스트에는 해당 숫자가 몇번 등장하는 지 횟수가 저장되는 것이다. 마지막으로 출력과정에서 카운트 한 갯수만큼 인덱스를 출력해주면 정렬이 완료되는 것이다.
0 0 1 1 2 2 3 4 5 5 6 7 8 9 9
계수 정렬의 시간 복잡도를 계산해보면 다음과 같다.
모든 데이터가 양의 정수 혹은 0인 상황에서 데이터의 개수를 N, 데이터 중 최댓값의 크기를 K라고 할 때, 시간 복잡도는 O(N+K) 이다. 계수 정렬에서는 반복문이 2번 등장하는데, 먼저 데이터가 몇번 등장하는지를 카운트하면서 1번 => (N) 만큼, 데이터를 출력하는 과정에서 최댓값의 크기만큼 반복 1번 => (K)만큼 반복되기 때문이다. 따라서 데이터의 범위만 한정되어 있다면 매우 빠른 정렬 알고리즘이라고 할 수 있는 것이다.
계수 정렬의 공간 복잡도에 대해서는 다음과 같다.
시간적인 측면에서는 매우 효과적이지만, 쓸데없는 메모리를 많이 차지할 수도 있다. 예를 들어 데이터가 2개인 경우를 생각해보자. 데이터가 0과 1 뿐이라면 매우 빠르고, 공간도 적게 차지할 것이다. 그러나 데이터가 0과 1,000,000으로 2개만 있다면 새로 만드는 리스트의 범위를 0 부터 1,000,000을 표현하기 위해서 1,000,001개의 요소를 가지는 리스트를 만들어야 한다. 따라서 공간 복잡도 측면에서 심각한 비효율성을 초래할 수 있는 것이다. 따라서 항상 사용할 수 있는 알고리즘은 아니라는 것이 다시 한번 느껴진다. 공간 복잡도는 O(N+K)이다.
다시 말해서 계수 정렬은 데이터의 크기가 한정되어 있고, 데이터가 많이 중복되어 있을 수록 유리한 정렬이다. 또한 조건에 부합하지 않다면 항상 사용할 수 없는 것이 단점인 정렬 알고리즘이다.
'Algorithm' 카테고리의 다른 글
| 정렬 (Sorting) (6) - 실전문제 6.2) 위에서 아래로 (0) | 2023.08.05 |
|---|---|
| 정렬 (Sorting) (5) - 파이썬의 정렬 라이브러리 (0) | 2023.08.05 |
| 정렬 (Sorting) (3) - 퀵 정렬 (Quick Sort) (0) | 2023.08.05 |
| 정렬 (Sorting) (2) - 삽입 정렬 (Insertion Sort) (0) | 2023.08.05 |
| 정렬 (Sorting) (1) - 선택 정렬 (Selection Sort) (0) | 2023.08.05 |
계수 정렬 (Count Sort) 은 매우 빠른 정렬 알고리즘이다. 그러나 한 가지 치명적인 약점이 있는데 바로 특정한 조건이 부합할 때만 사용할 수 있다는 것이다. 그 약점은 바로 '데이터의 크기 범위가 제한되어 정수 형태로 표현할 수 있을 때만 사용가능하다' 라는 것이다. 만약 데이터가 무한한 범위를 가질 수 있는 실수형 데이터라면 이 계수 정렬을 사용하기 힘들다는 것이다. 또한 일반적으로 가장 작은 데이터와 가장 큰 데이터의 값의 차이가 1,000,000을 넘지 않을 때 효과적으로 사용할 수 있다.
계수 정렬은 일반적으로 별도의 리스트를 선언하고 그 안에 정렬에 대한 정보를 담는다는 특징이 있다. 즉, 앞서 다루었던 정렬 알고리즘과는 다르게 직접 데이터의 값을 비교한 뒤에 위치를 변경하는 정렬 방식(비교 기반의 정렬 알고리즘)이 아니라는 것이다. 계수 정렬은 별도의 리스트를 선언한다고 했는데 이 리스트는 모든 범위를 담을 수 있는 크기의 리스트여야 한다. 만약 최소 데이터와 최대 데이터의 값의 차이가 1,000,000이라면 0 ~ 1,000,000을 모두 담아야 하므로 1,000,001 의 크기의 리스트를 선언해야 한다는 것이다.
아래와 같은 데이터를 계수 정렬하는 과정을 살펴보자.
7 5 9 0 3 1 6 2 9 1 4 8 0 5 2
여기서 가장 큰 데이터는 9, 가장 작은 데이터는 0 이므로 0 ~ 9 를 표현할 크기가 10인 리스트를 새로 선언한다.
이후 각 데이터의 개수를 카운트해서 새로 선언한 리스트에 저장하는 것이다. 이 과정을 거치면 새로 선언한 리스트에는 아래와 같은 값이 저장된다.
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 2 | 2 | 2 | 1 | 1 | 2 | 1 | 1 | 1 | 2 |
결과적으로 위의 리스트에는 해당 숫자가 몇번 등장하는 지 횟수가 저장되는 것이다. 마지막으로 출력과정에서 카운트 한 갯수만큼 인덱스를 출력해주면 정렬이 완료되는 것이다.
0 0 1 1 2 2 3 4 5 5 6 7 8 9 9

계수 정렬의 시간 복잡도를 계산해보면 다음과 같다.
모든 데이터가 양의 정수 혹은 0인 상황에서 데이터의 개수를 N, 데이터 중 최댓값의 크기를 K라고 할 때, 시간 복잡도는 O(N+K) 이다. 계수 정렬에서는 반복문이 2번 등장하는데, 먼저 데이터가 몇번 등장하는지를 카운트하면서 1번 => (N) 만큼, 데이터를 출력하는 과정에서 최댓값의 크기만큼 반복 1번 => (K)만큼 반복되기 때문이다. 따라서 데이터의 범위만 한정되어 있다면 매우 빠른 정렬 알고리즘이라고 할 수 있는 것이다.
계수 정렬의 공간 복잡도에 대해서는 다음과 같다.
시간적인 측면에서는 매우 효과적이지만, 쓸데없는 메모리를 많이 차지할 수도 있다. 예를 들어 데이터가 2개인 경우를 생각해보자. 데이터가 0과 1 뿐이라면 매우 빠르고, 공간도 적게 차지할 것이다. 그러나 데이터가 0과 1,000,000으로 2개만 있다면 새로 만드는 리스트의 범위를 0 부터 1,000,000을 표현하기 위해서 1,000,001개의 요소를 가지는 리스트를 만들어야 한다. 따라서 공간 복잡도 측면에서 심각한 비효율성을 초래할 수 있는 것이다. 따라서 항상 사용할 수 있는 알고리즘은 아니라는 것이 다시 한번 느껴진다. 공간 복잡도는 O(N+K)이다.
다시 말해서 계수 정렬은 데이터의 크기가 한정되어 있고, 데이터가 많이 중복되어 있을 수록 유리한 정렬이다. 또한 조건에 부합하지 않다면 항상 사용할 수 없는 것이 단점인 정렬 알고리즘이다.
'Algorithm' 카테고리의 다른 글
| 정렬 (Sorting) (6) - 실전문제 6.2) 위에서 아래로 (0) | 2023.08.05 |
|---|---|
| 정렬 (Sorting) (5) - 파이썬의 정렬 라이브러리 (0) | 2023.08.05 |
| 정렬 (Sorting) (3) - 퀵 정렬 (Quick Sort) (0) | 2023.08.05 |
| 정렬 (Sorting) (2) - 삽입 정렬 (Insertion Sort) (0) | 2023.08.05 |
| 정렬 (Sorting) (1) - 선택 정렬 (Selection Sort) (0) | 2023.08.05 |
