퀵 정렬 (Quick Sort) 는 매우 빠른 정렬 알고리즘으로 널리 알려져 있으며 대부분 프로그래밍 언어에서 정렬 라이브러리의 근간이 되는 알고리즘이다. 퀵 정렬이란 기준 데이터를 설정하고 그 기준보다 큰 데이터와 작은 데이터의 위치를 바꾸는 방식으로 정렬을 진행하는 알고리즘이다. 퀵 정렬에서는 기준이 필요하다. 이 기준은 피벗 (Pivot) 이라고 부른다. 먼저 피벗을 설정하고 피벗보다 큰 수와 작은 수를 교환한 후 리스트를 반으로 분할하는 방식으로 진행된다.
피벗을 선정할 때는 명확한 기준이 필요하고 그 기준을 명시해야 한다. 리스트의 첫 번째 데이터를 피벗으로 설정하는 호어 분할 (Hoare Partition) 방법으로 퀵 정렬을 이해한다. 먼저 아래와 같은 데이터가 있다고 가정한다.
5 7 9 0 3 1 6 2 4 8
여기서 호어 분할에 의해서 첫 번째 데이터인 5를 피벗으로 선정하고, 2번째 요소부터 뒤로 접근하면서 5보다 큰 데이터를 찾는다. 이 때 7이 탐색된다. 또한 마찬가지로 가장 마지막 요소부터 앞으로 접근하면서 피벗보다 작은 데이터를 찾으면 4를 찾는다. 이후 찾은 7과 4의 위치를 서로 바꾼다.
5 4 9 0 3 1 6 2 7 8
또 다시 위의 과정을 실행하면 5보다 큰 9, 5보다 작은 2가 선택될 것이고 둘의 자리를 바꾼다.
5 4 2 0 3 1 6 9 7 8
다시 위의 과정을 실행한다. 5보다 큰 수는 6이고 5보다 작은 수는 1이 선택됨을 알 수 있다. 이 때 데이터를 찾는 과정에서 앞에서 부터 뒤로 / 뒤에서부터 앞으로 찾으면서 인덱스가 겹쳐서 엇갈리게 되는데 두 인덱스가 엇갈리는 경우에는 작은 데이터와 피벗의 위치를 교환한다.
1 4 2 0 3 5 6 9 7 8
위의 과정처럼 엇갈렸을 때 작은 데이터와 피벗의 위치를 교환하게 되면 이제 원래 피벗이던 5보다 작은 숫자들이 5의 앞에 존재하고, 5보다 큰 숫자들은 5보다 뒤에 존재하게 된다. 이렇게 데이터를 위치시키는 작업을 분할 (Divide) 혹은 파티션 (Partition) 이라고 부른다. 이 상태에서 기존 피벗의 왼쪽 리스트와 오른쪽 리스트를 나눠서 다시 정렬시키면 전체 리스트에 대한 정렬이 완료되는 것이다.
왼쪽 리스트에서 피벗을 1로 설정하고 위의 과정과 동일한 과정을 거쳐서 왼쪽 리스트가 정렬되는 모습이다.
1 4 2 0 3 (초기, 피벗 = 1)
1 0 2 4 3
0 1 2 4 3 (인덱스 엇갈림)
기존 피벗(1) 의 왼쪽 리스트는 요소가 한 개이므로 이미 정렬 되었다고 판단, 1의 오른쪽 리스트에 퀵 정렬 진행
2 4 3 (초기, 피벗 =2)
2 4 3 (인덱스 엇갈림, 2(피벗)와 2(피벗보다 작거나 같은 데이터)의 자리 바꿈)
기존 피벗(2) 의 왼쪽 리스트는 요소 0개, 오른쪽 리스트는 요소 2개 이므로 오른쪽 리스트에 퀵 정렬 진행
4 3 (초기, 피벗=4)
3 4 (인덱스 엇갈림)
따라서 기존의 리스트는 아래와 같아질 것이다.
0 1 2 3 4 5 6 9 7 8
이후 가장 처음의 피벗이였던 5의 오른쪽 리스트에도 동일하게 퀵 정렬을 마저 해주면 리스트의 모든 요소에 대한 오름차순 정렬이 완료될 것이다.
0 1 2 3 4 5 6 7 8 9
퀵 정렬은 이처럼 리스트에서 특정한 기준을 통해서 피벗을 설정한 이후에 정렬을 수행한다. 이후, 인덱스가 엇갈림으로써 피벗의 왼쪽 리스트에는 피벗보다 작은 수, 오른쪽에는 큰 수만 남게 되는데 이 왼쪽 리스트와 오른쪽 리스트에 각각 다시 정렬을 수행한다. 이는 재귀 함수로 간단하게 구현할 수 있음을 알 수 있다. 이 때 종료조건은 '정렬을 수행하려는 리스트의 요소 개수가 0개 혹은 1개'로 설정할 수 있다. 이는 즉 이미 정렬이 완료된 리스트이기 때문이다.

아래의 코드는 파이썬의 슬라이싱 기능과 리스트 표현식을 통한 왼쪽 리스트, 오른쪽 리스트 할당을 포함하여 소스코드를 간단하게 줄인 코드이다.
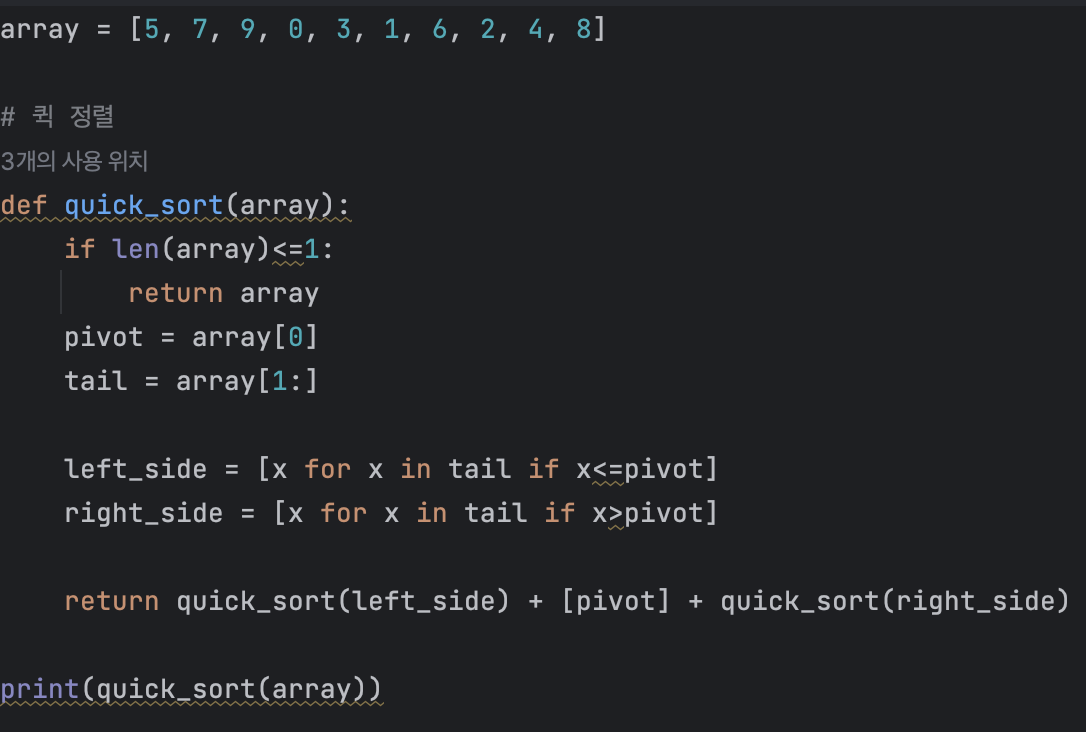
퀵 정렬의 시간 복잡도에 대해 알아보자. 앞선 게시물에서 구했듯이 선택 정렬과 삽입 정렬은 모두 시간 복잡도가 O(N^2) 임을 알게 되었다. 이들은 최악의 경우에서도 O(N^2)를 보장한다. 그러나 퀵 정렬의 평균 시간 복잡도는 O(NlogN) 이다. 앞의 두 정렬 알고리즘보다 수행 시간 측면에서 매우 빠른 편이다. (일반적으로 컴퓨터 과학에서 log의 의미는 밑이 2인 로그를 의미한다.)
데이터의 개수가 많을 수록 그 차이는 매우 크게 나타난다. 데이터의 크기에 따른 선택, 삽입 정렬과 퀵 정렬의 차이는 아래와 같다.
| 데이터 개수 (N) | 선택, 삽입 정렬 (N^2) | 퀵 정렬 (NlogN) |
| 1,000 | 1,000,000 | 10,000 |
| 1,000,000 | 1,000,000,000,000 | 20,000,000 |
이렇듯 매우 빠르게 정렬할 수 있는 알고리즘인 퀵 정렬도 최악의 경우에는 시간 복잡도가 O(N^2) 을 가질 수 있다. 만약 데이터가 이미 정렬되어 있는 경우에는 가장 왼쪽 데이터를 피벗으로 설정하여 정렬하므로 매우 느리게 동작할 수 있는 것이다. 이미 데이터가 정렬되어 있을 때 매우 효과적인 삽입 정렬과는 반대로 퀵 정렬은 효율이 떨어지게 되는 것이다.
'Algorithm' 카테고리의 다른 글
| 정렬 (Sorting) (5) - 파이썬의 정렬 라이브러리 (0) | 2023.08.05 |
|---|---|
| 정렬 (Sorting) (4) - 계수 정렬 (Count Sort) (0) | 2023.08.05 |
| 정렬 (Sorting) (2) - 삽입 정렬 (Insertion Sort) (0) | 2023.08.05 |
| 정렬 (Sorting) (1) - 선택 정렬 (Selection Sort) (0) | 2023.08.05 |
| BFS (2) - 실전문제 5.4) 미로 탈출 (0) | 2023.08.01 |
