그래프란 자료 구조의 한 종류로 노드 (node) 와 간선 (edge) 으로 표현되는 구조이다. 이 때, 노드를 정점 (vertex) 이라고 부르기도 한다. 아래에 3개의 그래프에 대한 예시를 보자.
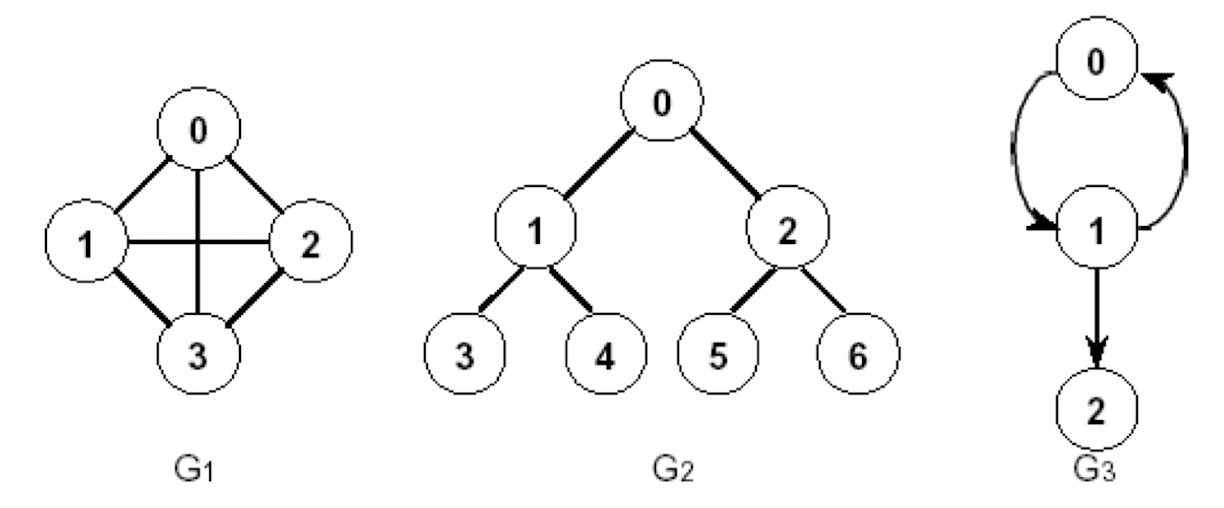
이 3개의 그림 모두 그래프를 표현한 것이다. 먼저 G2는 트리 (Tree) 의 형태를 띄고 있다. 따라서 트리 또한 (순환하지 않는) 그래프의 한 종류라는 것을 알 수 있다. G1과 G2에는 화살표가 존재하지 않고, G3에는 화살표가 존재하는 것을 알 수 있다. 이는 undirected graph (무방향 그래프)와 directed graph (유방향 그래프) 의 차이이다.
- Undirected Graph : 방향이 없는 간선을 가지고 양방향 관계를 나타내는 간선을 가지는 그래프
- Directed Graph : 방향이 있는 간선을 가지고 단방향 관계를 나타내는 간선을 가지는 그래프
쉽게 이야기 하면 예를 들어 G1은 undirected graph라 노드1에서 노드0, 노드2, 노드3으로 갈 수 있지만 G3는 directed graph이기 때문에 노드2에서 노드1로 갈 수 없는 것이다.
그래프에서의 제약사항은 아래와 같다.
- (a) vertex i 에서 자기 자신 (vertex i) 으로 향하는 edge는 존재할 수 없다. ( self loop는 허용되지 않는다. )
- (b) 동일한 vertex간의 edge는 여러개 존재할 수 없다.


그래프의 자료구조에서 사용하는 용어를 간단히 설명하면 다음과 같다.
- 경로 (path) : vertex i를 출발하여 vertex j로 가는 edge의 조합이 존재한다면 경로가 존재한다고 한다.
- 경로의 길이 (length of path) : 경로 상의 edge의 개수
- 단순 경로 (simple path) : 같은 vertex를 두 번 이상 방문하지 않는 경로
- 순환 (cycle) : 처음과 끝의 vertex가 동일한 경로
- 연결된 정점 (connected vertex) : vertex끼리 path가 존재
- 연결된 그래프 (connected graph) : 모든 vertex끼리 path가 존재
- 하위 그래프 (subgraph) : 그래프의 일부분, vertex 한 개 또한 하위 그래프가 될 수 있음
- 차수 (degree) : 해당 vertex에 연결된 edge 개수
- in-degree : [directed graph에서] 해당 vertex로 들어오는 edge 개수
- out-degree : [directed graph에서] 해당 vertex에서 나가는 edge 개수
'Algorithm' 카테고리의 다른 글
| 자료구조 (Data Structure) (6) - 그래프 표현 방식 : 인접 리스트 (Adjacency List) (0) | 2023.07.30 |
|---|---|
| 자료구조 (Data Structure) (5) - 그래프 표현 방식 : 인접 행렬 (Adjacency Matrix) (0) | 2023.07.30 |
| 재귀 함수 (3) - 재귀 함수의 대표적인 예 : 팩토리얼 (Factorial) (0) | 2023.07.30 |
| 재귀 함수 (2) - 재귀 함수의 종료 조건 (0) | 2023.07.30 |
| 재귀 함수 (1) - 재귀 함수 (Recursive Function) 란? (0) | 2023.07.30 |
